狭义相对论力学，探索四维时空中的守恒性(2)

得到

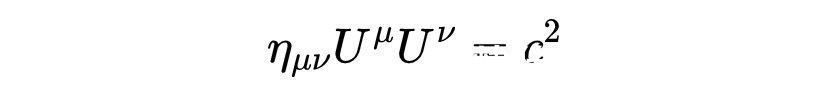
这显然是一个不变量。

相对论动量

在牛顿力学中，一个粒子的动量等于这个粒子的质量m乘以它的普通空间速度v：

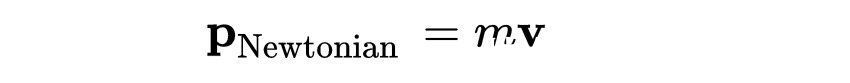
空间速度有分量

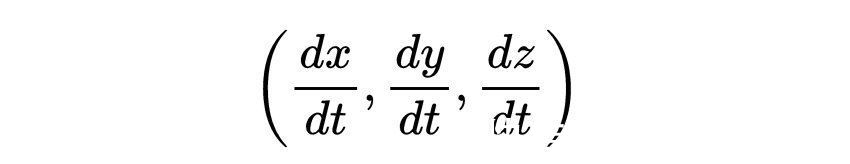
如果牛顿系统（速度远小于光速）没有外力作用，动量是守恒的。在狭义相对论中，速度在不同的惯性系之间以复杂的方式变换，因此我们不能使用牛顿动量守恒定律。相反，我们需要引入相对论动量的概念。为了做到这一点，我们用固有时代替坐标时间t，并定义相对论动量p为

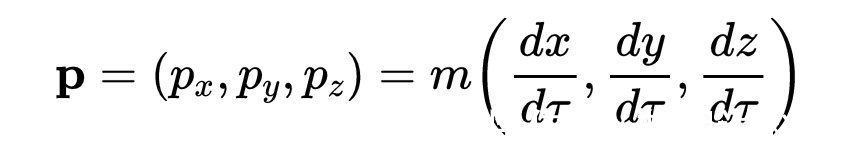
因为我们已经知道

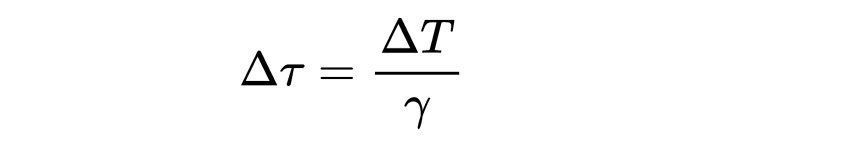
我们可以把p用坐标时间表示为

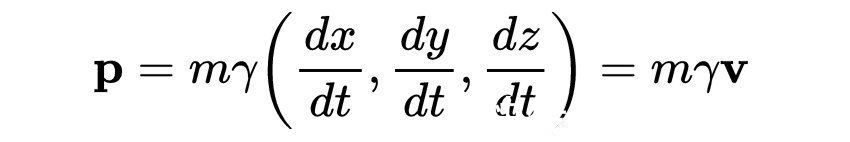
它会通过洛伦兹变换在不同的惯性系之间变换。重要的是，这意味着和牛顿动量不同，相对论动量在所有惯性系中都是守恒的。

相对论动能

粒子的动能是它由于运动而拥有的能量。在牛顿力学中，质点m以速度v运动的动能定义为使质点从静止加速到速度v所做的功。做的功W等于力F乘以力作用的距离，也就是

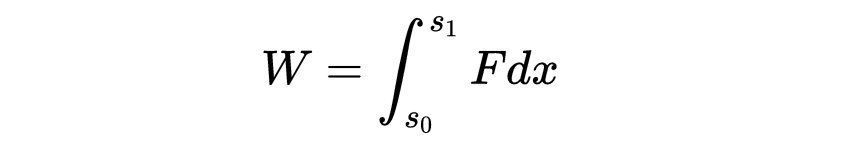
牛顿第二定律将力与质量和加速度联系起来F=ma。所以我们可以说所做的功是为

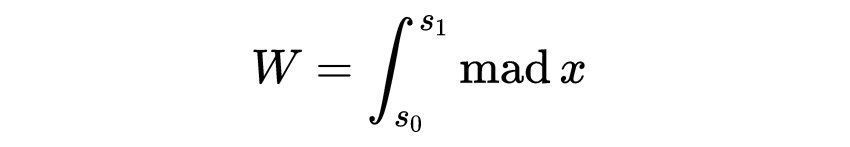
加速度是速度相对于时间的变化率，我们可以把它代入上面的方程来得到

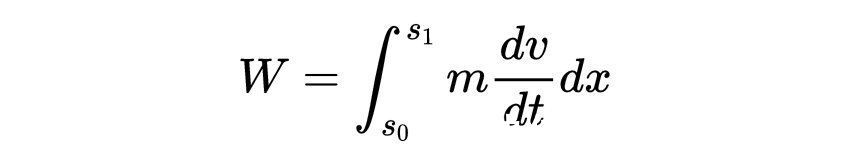
用链式法则可以写成

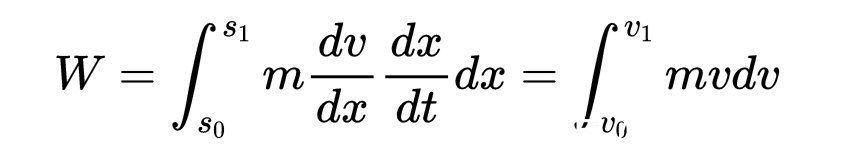
v_1是粒子在距离s_1处的速度。v_0是粒子距离s_0处的速度。因此积分得到

因为我们把动能定义为使粒子从静止加速到最终速度v所做的功，而v_0=0并且动能为

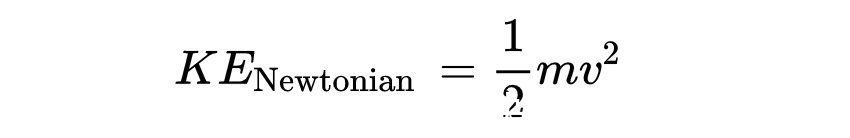
因为牛顿动量p = mv，我们可以重写一下功的计算公式

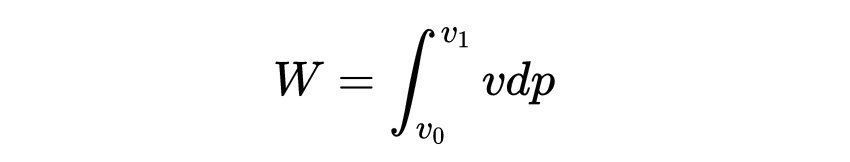
其中p_0和p_1分别是粒子的初始动量（= 0）和最终动量（=mv_1）。这给了我们一种方法来找到相对论动能。这给了我们一种找到相对论动能的方法，即用相对论动量代替牛顿动量

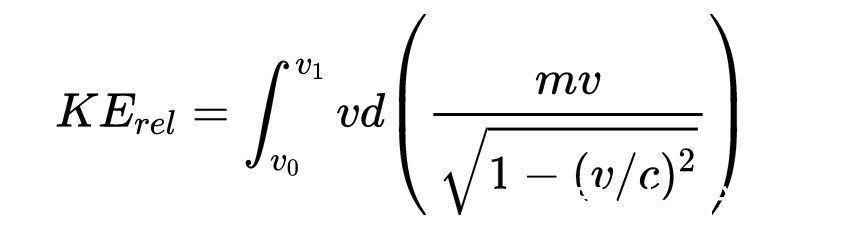
我们可以先用分部积分法求这个积分

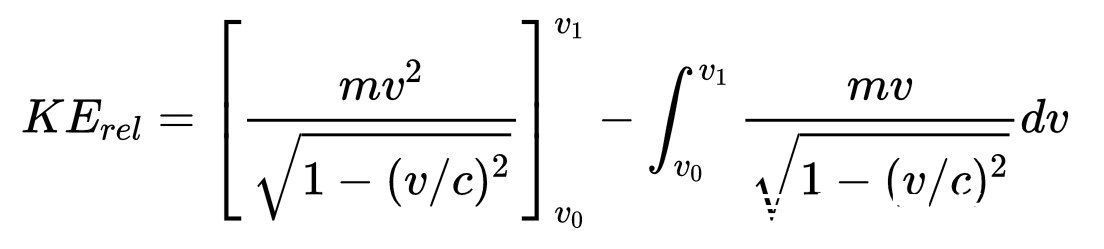
然后，我们需要在第二项上使用代换积分法。首先，提出常数m

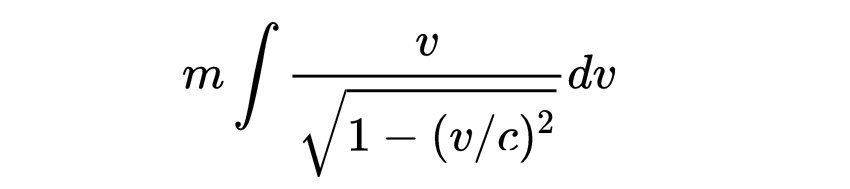
让

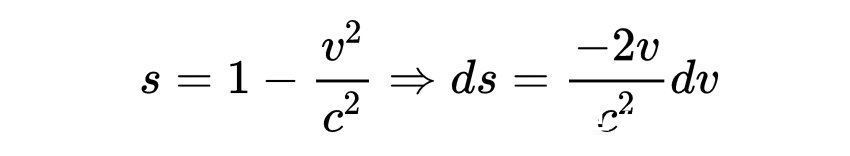
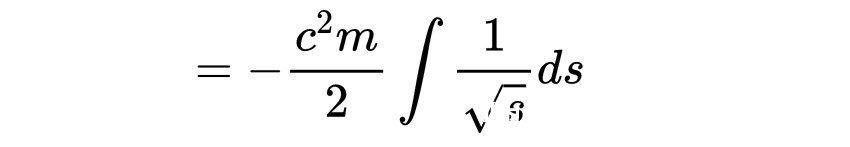
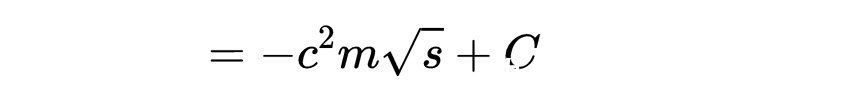
把s替换为

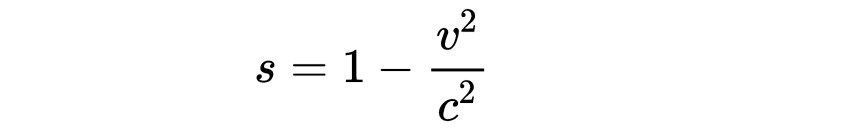
得到：

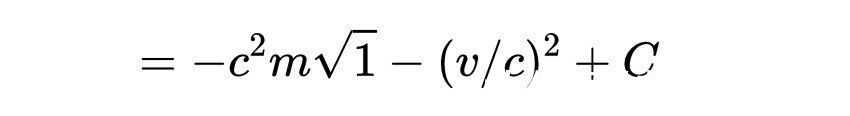
这意味着我们现在可以写出

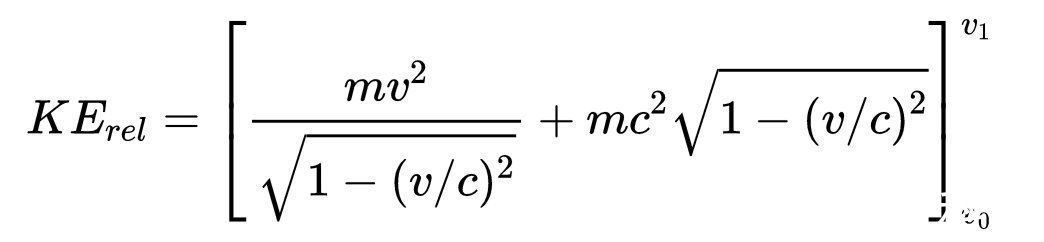
然后，右边项的顶部和底部乘以

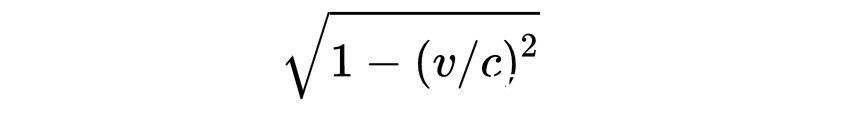
让所有的东西都有一个公分母

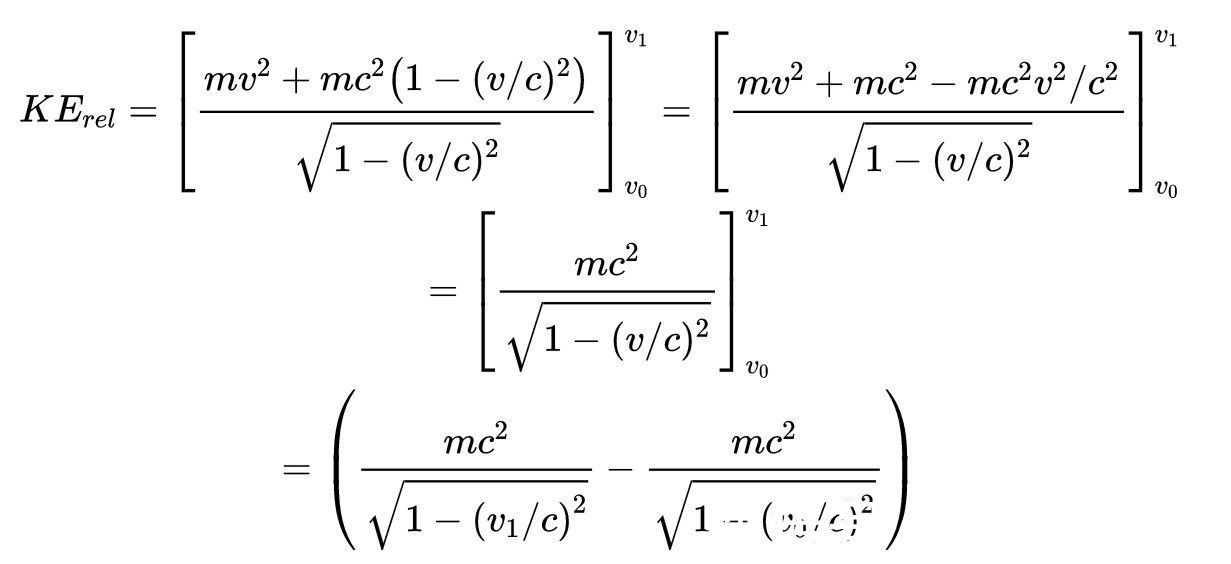
让v_1=v，我们知道粒子从静止开始加速，因此，我们最终得到了质量为m的粒子以速度v运动的相对论动能的方程：

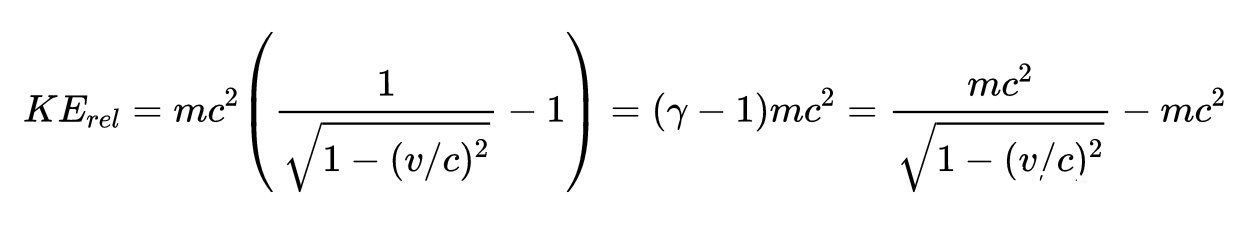
γ是洛伦兹因子。这看起来和牛顿动能方程很不一样。然而，使用泰勒定理可以展开洛伦兹因子

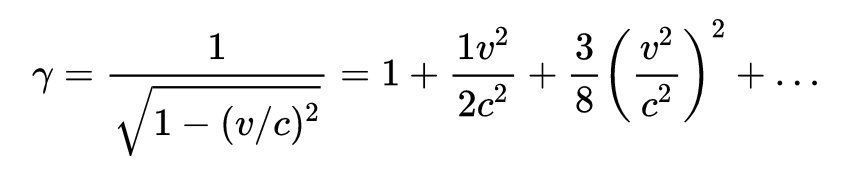
因此

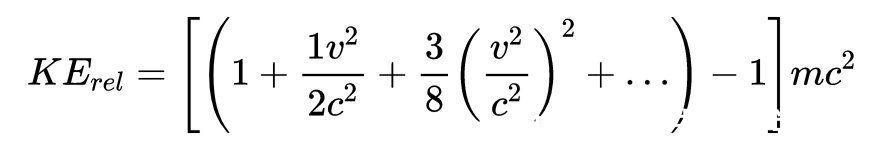
在牛顿系统中v＜＜c，因此忽略平方和更高次项，得到

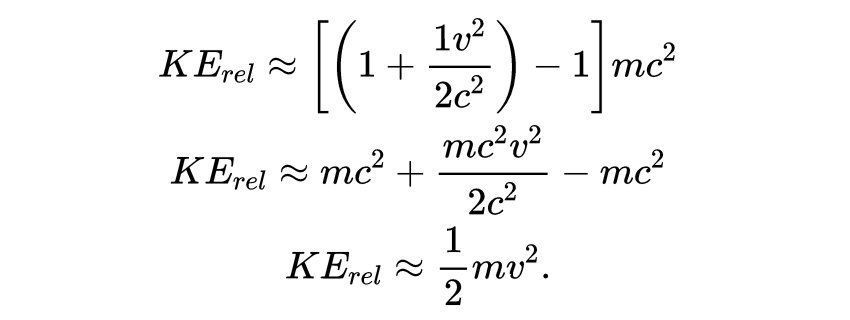
所以在低速时，相对论动能近似于牛顿动能。

总相对论能量