如果我们重新排列相对论动能的方程，可以写出

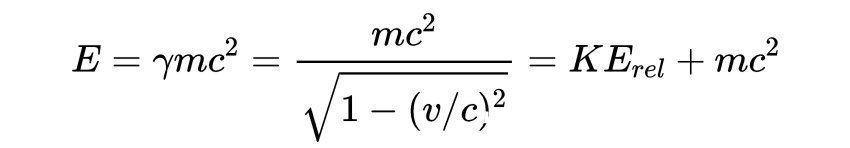
现在我们有了一个方程，它给出了一个粒子在惯性系中的总相对论能量E。总相对论能量由粒子的相对论动能加上第二项mc^2组成（粒子的质能）。它可以在理论上被证明，并且已经在实验上被证实，在没有外力作用的情况下，总的相对论能量在所有惯性系中是守恒的，无论质量或动能是守恒的。在高速粒子碰撞中，例如，质量，动能，甚至粒子的总数可能不守恒，但系统的总相对论能量会守恒。

若粒子静止，则洛伦兹因子减小为1，并且

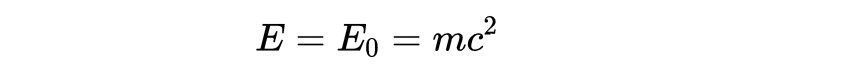
这是爱因斯坦著名的质能方程，该方程表明，质量和能量在某种意义上是相等的，即使在静止状态下，粒子仍然会因为其质量而拥有能量。显然，c^2是一个很大的数，所以少量的质量产生大量的能量。

四维动量

如果我们把四维速度乘以一个粒子的静止质量m，就得到另一个四维矢量，叫作四维动量：

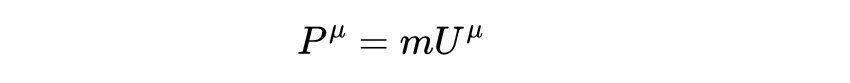
回想一下四维速度的定义

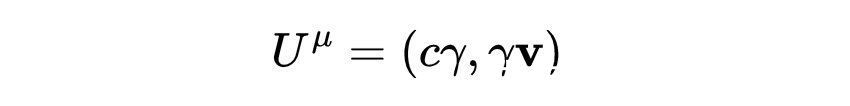
然后乘以m就得到

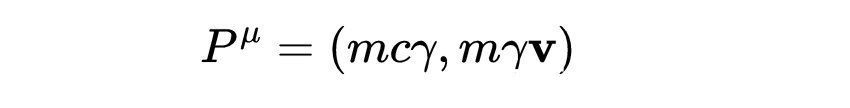
而E=γmc^2是相对论总能量，并且p=mγv是相对论动量的方程。我们可以看到mcγ是总相对论能量除以光速，因此四维动量可以重写为

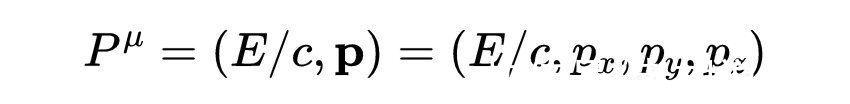
四动量提供了一个粒子的相对论总能量（它的时间分量）和相对论动量（它的空间分量）的完整描述。Schutz]总结了这一点，他说粒子的四动量是一个矢量，在某个坐标系中的分量给出了粒子相对于那个坐标系的能量和动量。正如我们以后会看到的，所有重要的能量-动量张量，即爱因斯坦场方程的右边和时空曲率的来源，实际上是四维动量单位面积上的流速的度量。

四维力

牛顿第二运动定律说，作用在物体上的力等于物体动量的变化率

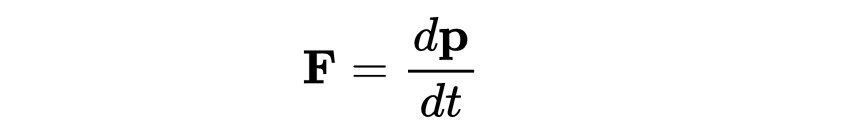
我们可以把它推广到狭义相对论，定义四维力为四维动量的变化率

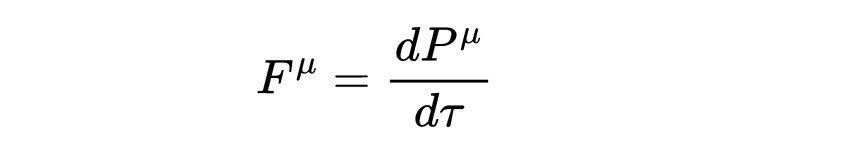
它展示了自由粒子如何在弯曲时空中运动。

能量动量关系

四维速度的标量积为：

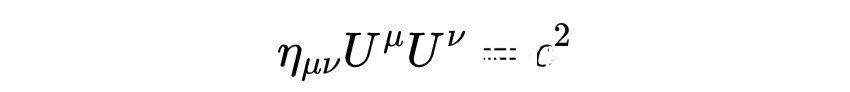
而四维动量为

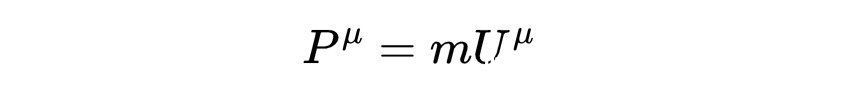
因此

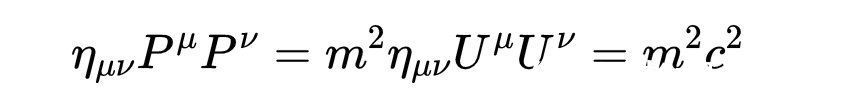
但是四维动量的标量积

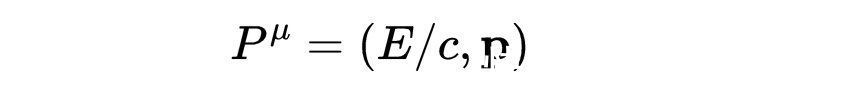
也可以从

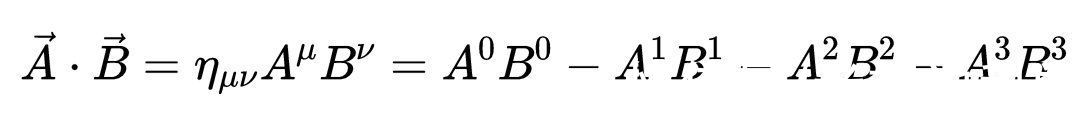
求得，为

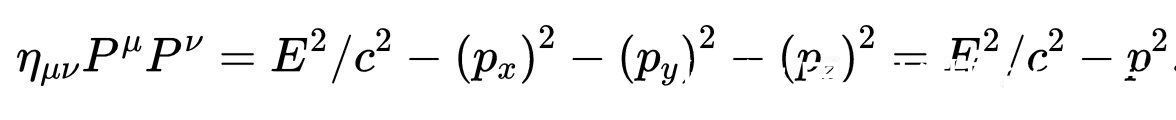
把这两个四维动量标量积的表达式结合起来，我们得到

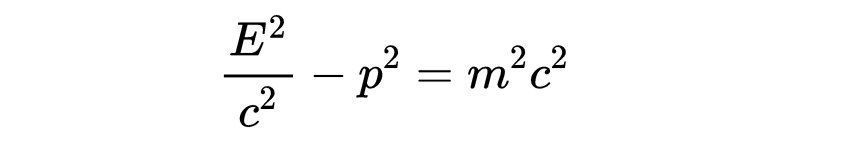
整理得

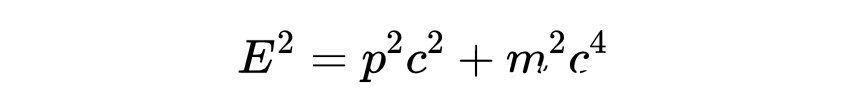
对于静止的质点（即动量为零的质点），这等于

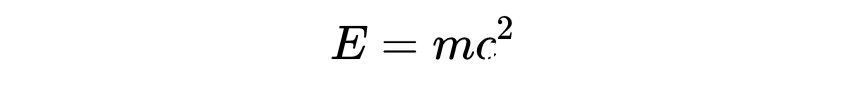
正如我们之前看到的，当我们看相对论总能量时，就是著名的质能方程。光（和其他电磁辐射）可以被认为是一束光子，一种基本粒子。一个“静止质量”为零的光子，确实有能量和动量。如果我们让m = 0进来，得到

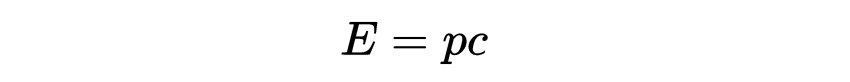
它描述了光子的能量动量关系。

文章来源：《实验力学》 网址: http://www.sylxzz.cn/zonghexinwen/2022/0108/751.html